이번 글은 그래프와 관련된 알고리즘 문제 풀이시 자주 사용되는 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS)에 대해 알아보려 한다.
우선 DFS에 대해 알아보자
깊이 우선 탐색(DFS)
깊이우선탐색 DFS는 깊이를 우선으로 하여 탐색하는 방법이다.
최대 깊이에 도달하면 직전의 갈림길로 돌아가기 때문에 후입선출의 구조를 가진 스택(Stack)을 사용한다.
DFS의 순서는 다음과 같다.
- 시작 노드를 결정하여 스택에 넣고 방문처리 한다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 존재한다면 그 노드를 스택에 넣고 방문 처리한다. 만약 인접한 모든 노드에 방문했다면 스택에서 최상단 노드를 꺼낸다.
- 2번의 과정을 수행할 수 없을 때 (모든 노드에 방문했을 때) 종료한다.
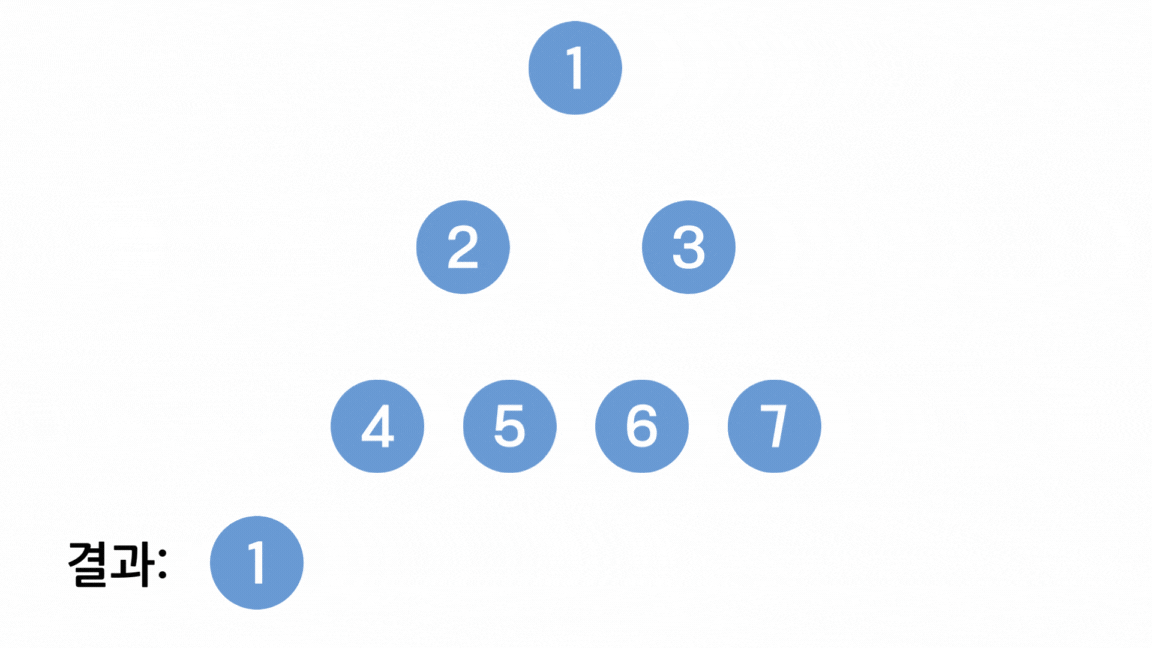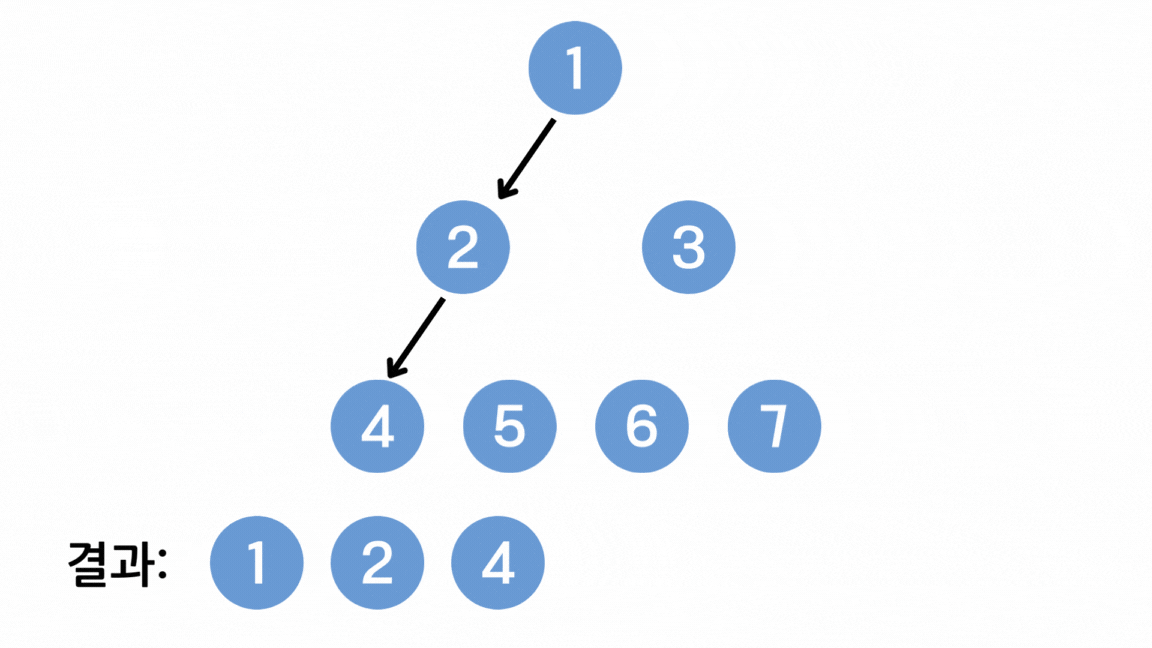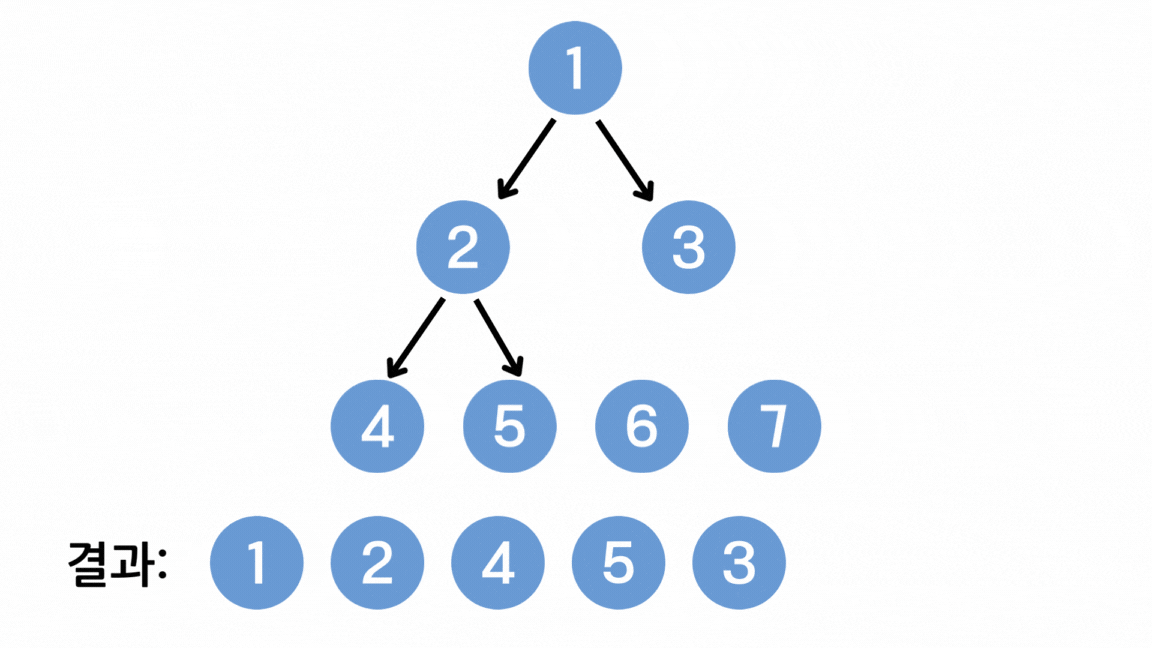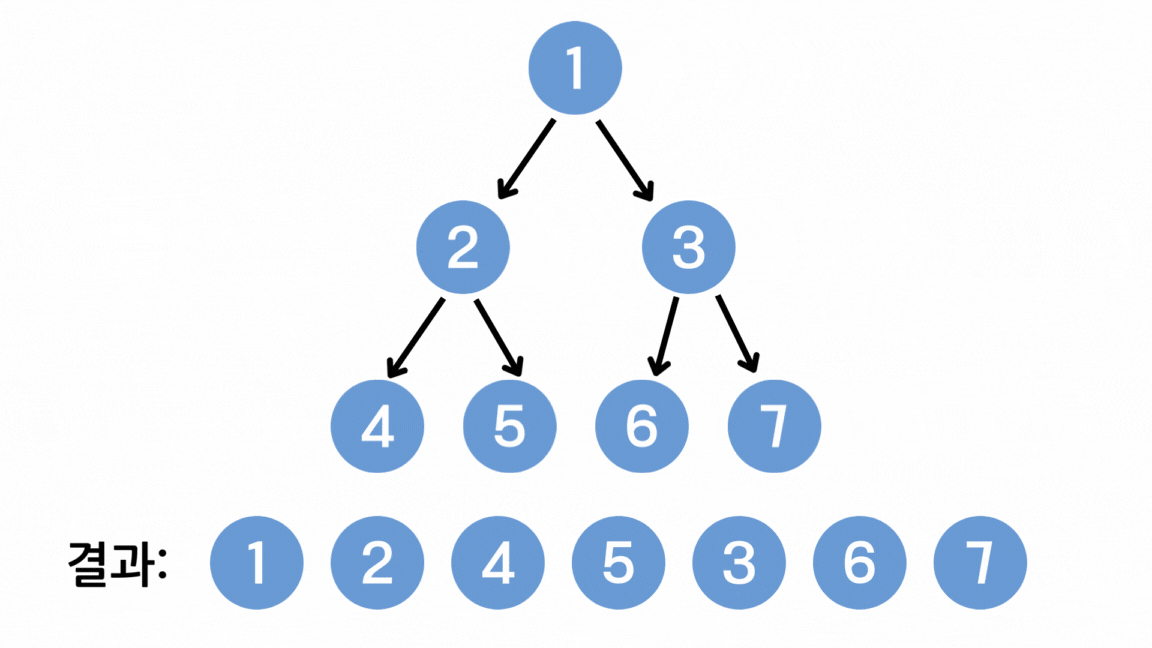
※ 편의를 위해 스택 구조로 설명했지만 DFS를 구현할 때 일반적으로 스택의 성질을 갖는 재귀함수를 사용한다.
그러면 기본적인 DFS 문제를 풀어보자 (백준 1260번. DFS와 BFS)
def dfs(num):
print(num, end=' ')
# 모든 노드 방문시 return
if sum(visited)==N:
return
# 작은 수 부터 방문하기 위해 정렬
lst = sorted(graph[num])
for i in lst:
if visited[i] == False:
visited[i] = True
dfs(i)
# N: 정점의 개수, M: 간선의 개수, V: 탐색을 시작할 번호
N, M, V = map(int, input().split())
# 인접리스트를 위한 빈리스트 만들기
graph = [[] for _ in range(N + 1)]
# DFS의 방문체크
visited = [False for _ in range(N + 1)]
# 인접리스트 채우기
for _ in range(M):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
visited[V] = True
dfs(V)
그렇다면 이번에는 BFS에 대해 알아보자
너비 우선 탐색(BFS)
너비우선탐색 BFS는 너비를 우선으로 하여 탐색하는 방법이다.
시작노드와 가까운 노드를 우선하여 탐색하므로 선입선출 구조를 가진 큐를 사용한다.
BFS의 순서는 다음과 같다.
- 시작 노드를 결정하여 큐에 넣고 방문처리 한다.
- 큐에서 노드를 꺼내어 인접한 노드를 모두 큐에 넣고 방문 처리한다. 인접한 노드에 모두 방문했는데 미방문된 노드가 남아있을 경우 큐에서 노드를 하나 꺼낸다.(선입선출 구조이므로 가장 처음 넣은 노드)
- 2번의 과정을 수행할 수 없을 때 (모든 노드에 방문했을 때) 종료한다.
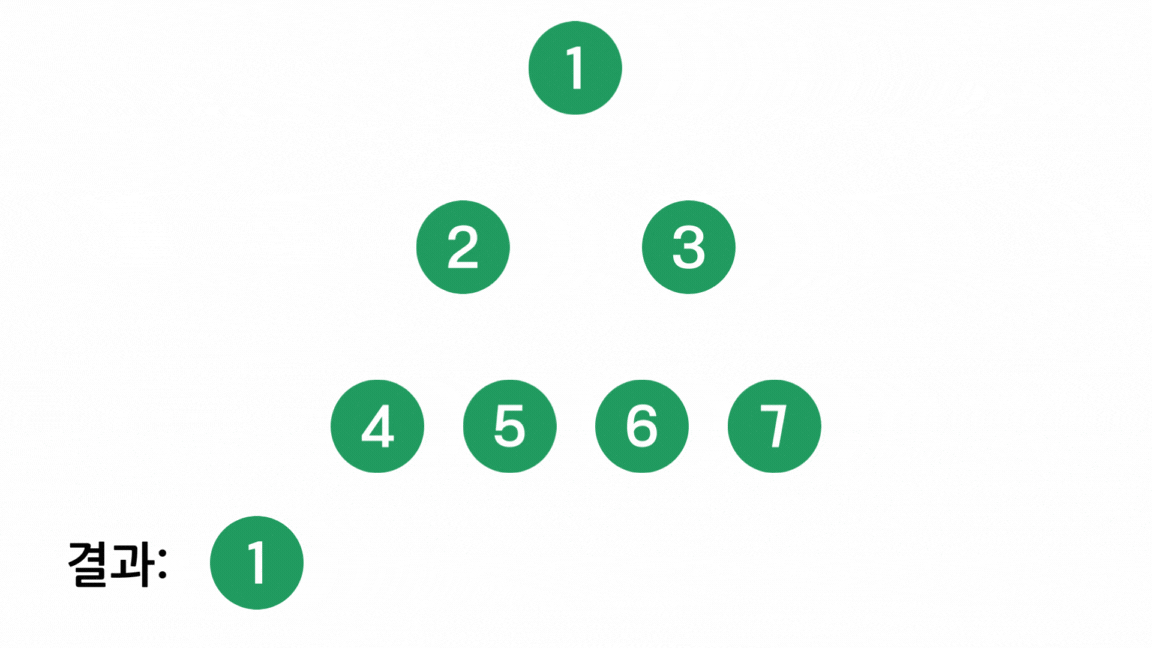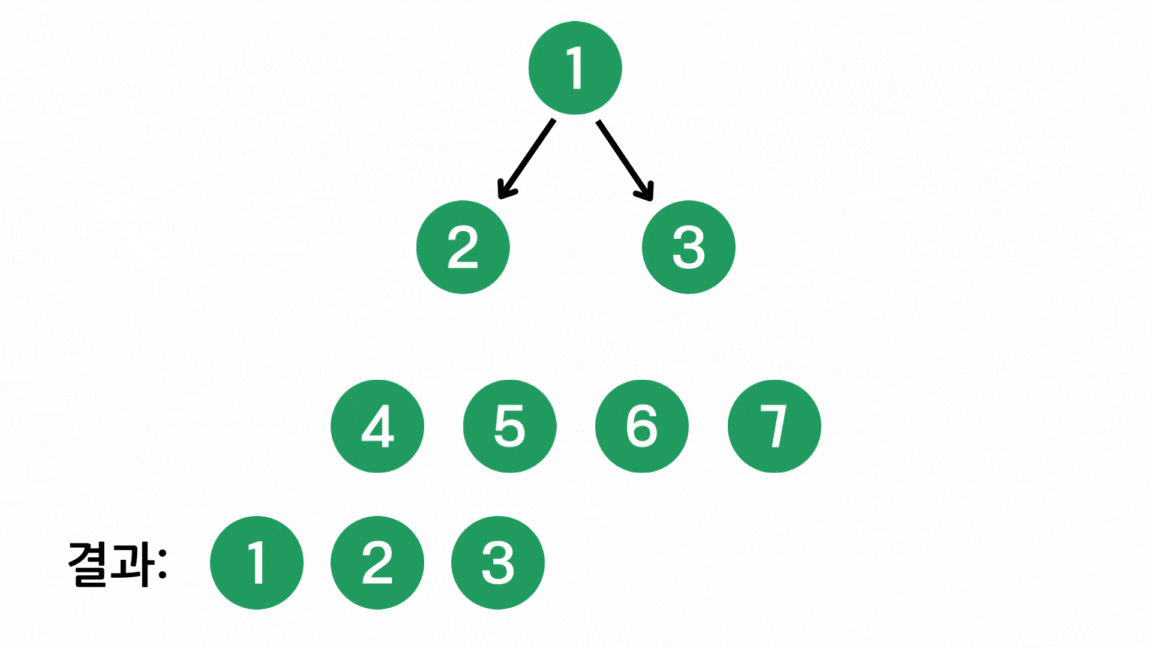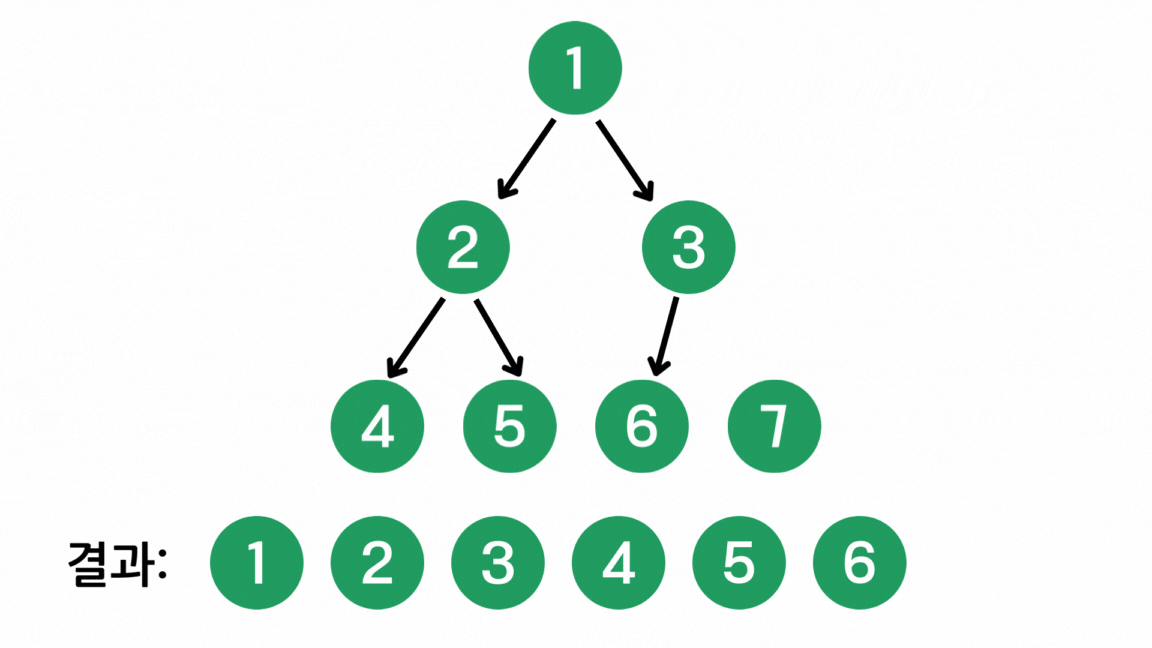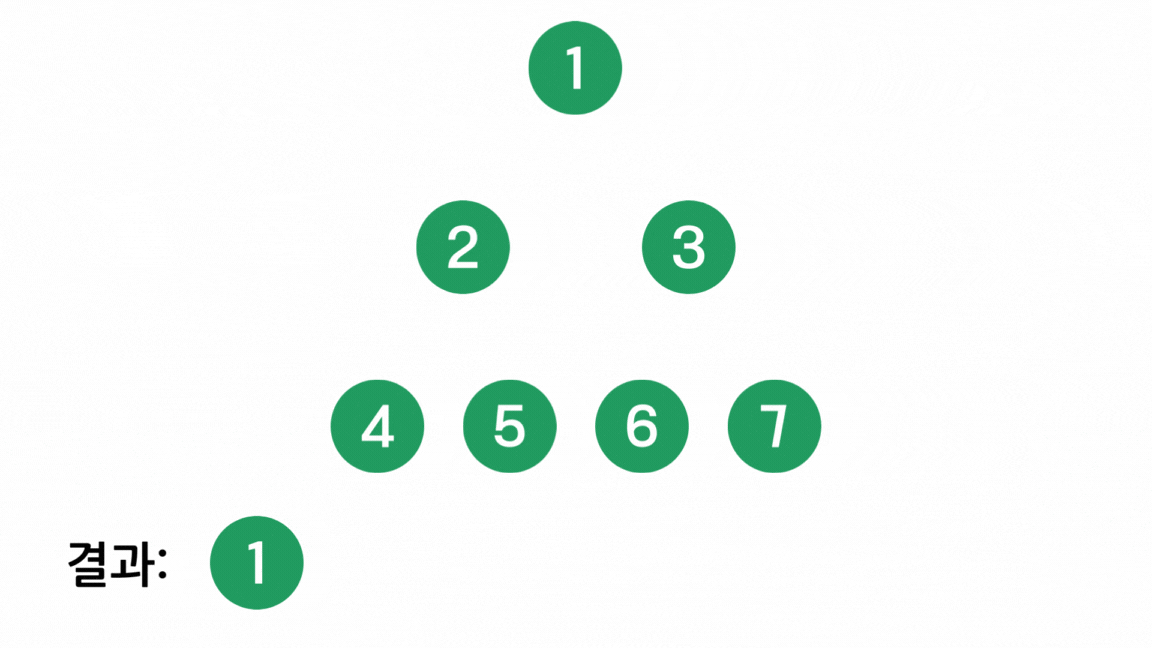
이제 기본적인 BFS 문제를 풀어보자 (백준 1260번. DFS와 BFS)
from collections import deque
def bfs(num):
q=deque()
q.append(num)
while q:
tm=q.popleft()
print(tm, end=' ')
lst=sorted(graph[tm])
for i in lst:
if visited2[i]==False:
q.append(i)
visited2[i]=True
# N: 정점의 개수, M: 간선의 개수, V: 탐색을 시작할 번호
N, M, V = map(int, input().split())
# 인접리스트를 위한 빈리스트 만들기
graph = [[] for _ in range(N + 1)]
# BfS의 방문체크
visited2 = [False for _ in range(N + 1)]
# 인접리스트 채우기
for _ in range(M):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
visited2[V]= True
bfs(V)DFS와 BFS의 차이
👍 DFS의 장점
- 현재 경로만 기억하기 때문에 BFS에 비해 메모리 소모가 적다.
👎 DFS의 단점
- 최단 경로를 보장하지 않는다.
👍 BFS의 장점
- 최단 경로를 보장할 수 있다.
👎 BFS의 단점
- 깊이가 깊을 경우 메모리가 많이 필요하다.
백준 1260번
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
'알고리즘' 카테고리의 다른 글
| [알고리즘] 유니온 파인드(Union Find) - 파이썬(python) (0) | 2023.05.05 |
|---|---|
| [알고리즘] 투 포인터와 슬라이딩 윈도우 - 파이썬(python) (0) | 2023.04.06 |
| [알고리즘] 순열과 중복순열, 조합과 중복조합 직접 구현하기 - 파이썬(python) (0) | 2023.03.31 |
댓글